
4 月 20 日,在机器之心「量子计算」线上圆桌活动中,机器之心邀请到了中科院计算所研究员、量子计算实验室主任孙晓明。他的演讲主题为《量子搜索算法与线路优化》,报告简要回顾了搜索算法和线路优化的发展以及目前面临的挑战,介绍了其团队在这两方面的一些工作进展。

演讲回顾视频(点击阅读原文查看):https://app6ca5octe2206.pc.xiaoe-tech.com/detail/p_62612f69e4b09dda125e441b/6?fromH5=true
机器之心对他的演讲内容做了不改变原意的编辑。
我今天想要介绍的是关于量子搜索算法与线路优化,重点介绍搜索这部分。众所周知,搜索是在经典计算机上面应用最广泛的算法之一,它可以应用于搜索引擎、路径导航或者推荐系统等。现在它还可以应用于新药的研发,甚至我们可以将密码破译看成一个搜索问题。
举例而言,我们想要破译一个哈希函数,相当于要搜到一个字符串,使得它哈希之后满足某一些特性,比如它的前 32 位都是 0,等等。我们知道,计算机算法界有一套被奉为圣经的图书——Knuth 所著的《计算机编程的艺术》(The Art of Computer Programming),它的整个第三卷都在讲 Sorting 和 Searching,由此可见搜索的重要性。

量子搜索算法
我们也知道,量子计算在 90 年代突然火了起来,其中一个重要的原因是两个重要算法的提出,即 Shor 算法和 Grover 算法。
Grover 算法
Grover 算法可以在一个无序的数据库上去查找一个特定的元素,比如想在一个数据库里查一个特定的 IP 地址,或者找一个哈希函数的原像,以及棋类游戏的最优策略,都可以看作一个搜索任务。

对于经典算法来说,在一个没有加过索引的数据库上,如果数据库的规模是 n 的话,那么肯定需要线性于 n 的时间。而量子算法可以有开平方量级的加速,它虽然没有像 Shor 算法那样能够达到一个指数规模的加速,但开平方在很多情况下其实也很有意义。比如说在大数据处理中,本来有 1 亿条的数据要处理,Grover 算法可以做到万这个量级。
再比如密码分析,原本是 2 的 90 次方的一个暴力枚举算法,我们可以降到 2 的 45 次方左右。对于现在的超算,2 的 45 次方的规模是可以接受的。

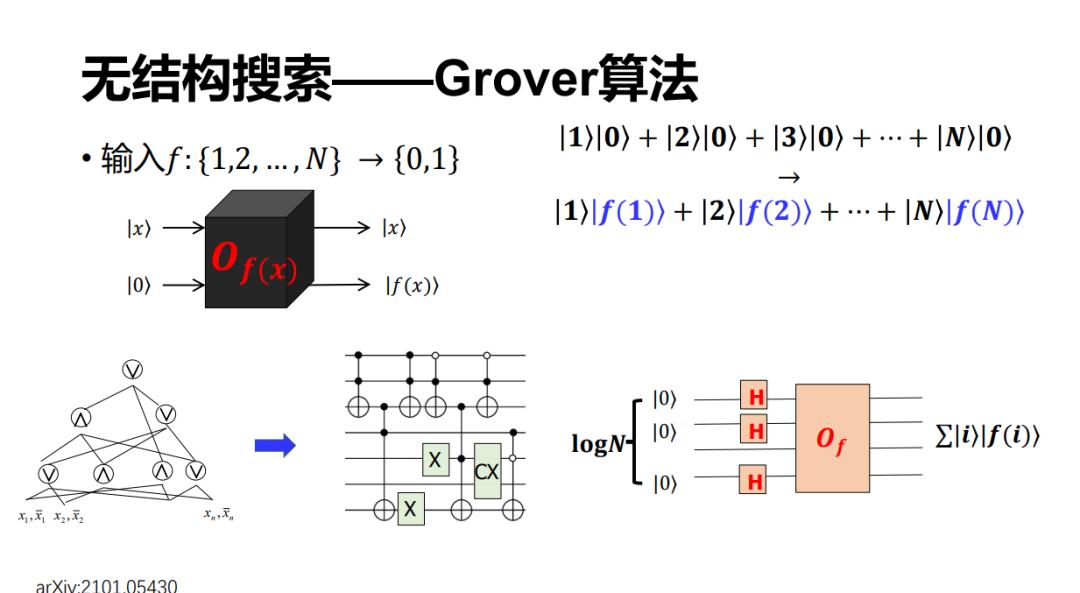
对于 Grover 搜索,它里面要用到一个很重要的模块——Oracle。我们经常会看到这样一种说法,如果有 50 个量子比特就可以实现 2 的 50 次方的并行加速,这件事情基本上是对的。他其实在说这样一件事情,如果可以制备 n 个比特的叠加态,譬如我们记 n 是 logN 的话,那么事先制备 n 个零态,然后做一个 Hardmard 变换之后,它就可以生成所有的从 1 到 N(或者从 0 到 N-1=2 的 n 次方减 1)个计算基的叠加态。然后根据线性性,它经过一个 Oracle 之后就可以计算全部的 f(x)(x=1~N),会得到这样一个态(图中包含蓝色的叠加态)。
这里其实有两个问题,剩余的报告里也会谈到,就是涉及到 Oracle 的制备,它是基于 QRAM 可以实现的角度。但在很多问题当中,这个 Oracle 是有具体的意义的,比如像我们刚才介绍过的,它可能是下图左上角的一个哈希函数,或者甚至是一个 NP 完全问题,比如一个 SAT 公式等。这样一个 oracle 该怎么制备呢?其实大家很早(例如 Nielsen 和 Chuang 的《Quantum Computation and Quantum Information》书中)就定性地知道:只要是一个可逆函数,那么都可以通过量子的方式实现出来。
最近,我们在 oracle 的定量实现方面做过这样一个工作,已经上传到了 arxiv 上。我们针对的是这样一类函数,即 CNF 或者 SAT oracle 的制备。
论文地址:https://arxiv.org/pdf/2101.05430.pdf
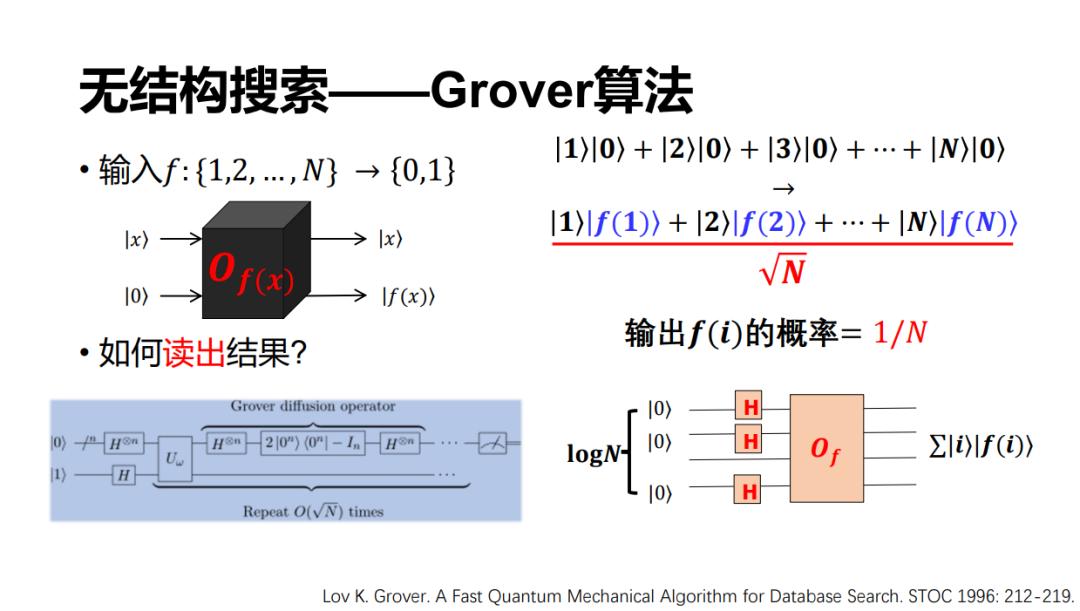
另外一个问题是怎么样读出计算结果?我们知道量子的测不准原理, 2^n个结果是不可能一次全部读出来的,每次读出来的概率其实只有1/2^n,这意味着如果有50个比特的话,每次只有 1/2^50 的概率看见任何一个结果。如果想要拿到特定的计算结果,又要花 2^50 的时间重复测量,所以这里量子就没有产生加速。
但是,Grover 算法很巧妙的设计了一个通过若干次的对称和反转,然后只需要根号 N 的时间,就能够以高概率拿到我们想要的结果。
振幅放大算法
在 Grover 之后,理论工作者又提出了一个被称为振幅放大的算法,它想要解决的是这样一个场景:如果现在有一个随机搜索算法,它的成功率可能比较低,比如万分之 1。我们希望通过调用这个算法来拿到一个高的成功概率。
古人常说,「三个臭皮匠顶个诸葛亮」。如果每一个算法的成功概率是万分之 1,那么我们平均要重复 1 万次。但是,使用振幅放大算法的思想(它和 Grover 很像)可以做到开平方,也就是说本来要 1 万次,其实只需要大约 100 次这个量级就可以做成。
当然这需要事先把这个算法变成一个量子算法,然后才可以产生这样一个加速。比如说我们把它应用到刚才说的 NP 完全问题或 SAT 问题上,如果随机地选一个解,成功的概率是 1/2^n。所以,如果只是简单粗暴地使用一下 Grover 算法,就可以做到根号 2 的 n 次方,也就 1.414^n。
但是还可以再加一些算法设计的技巧,这是因为刚才只是简单地调用一下 Grover 算法,并没有任何算法的技术在里面。假如做一些更好的算法设计,并使用一些更好的 SAT 求解算法的话,事实上复杂性可以做到比原来要小很多。

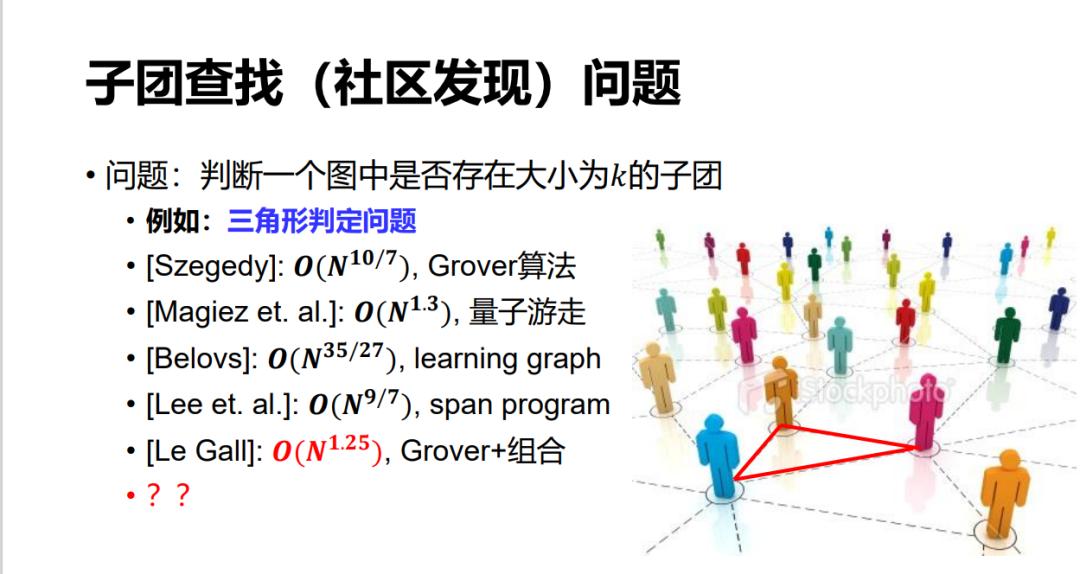
另外还有一些问题,比如在大数据里,我们经常想在一个社区里找一个子团,哪怕是找一个三角形这样最简单的子团。其实,这个问题到现在都不知道它最好的量子算法可以做到什么程度。
如果简单地用 Grover 算法可以做一个 n^1.5 的算法,因为三角形一共最多是 n^3,所以 Grover 就可以做 n^1.5。后来 Szegedy 可以做到 n^10/7,到现在可以做到 n^5/4。但是否还有更好的,我们尚不清楚。
这其实给我们一个启示,即很多人在问的量子算法为什么设计起来比较难。在我看来,一个方面的原因是量子确实有一点反直观,它不像我们经典世界那样看得见摸得着,所以设计起来是有不小的难度。另一方面目前从事该方向研究的人员还很不足,纽约时报的一个报道称全世界从事量子计算的专家不超过一千人。
研究成果介绍
局部搜索
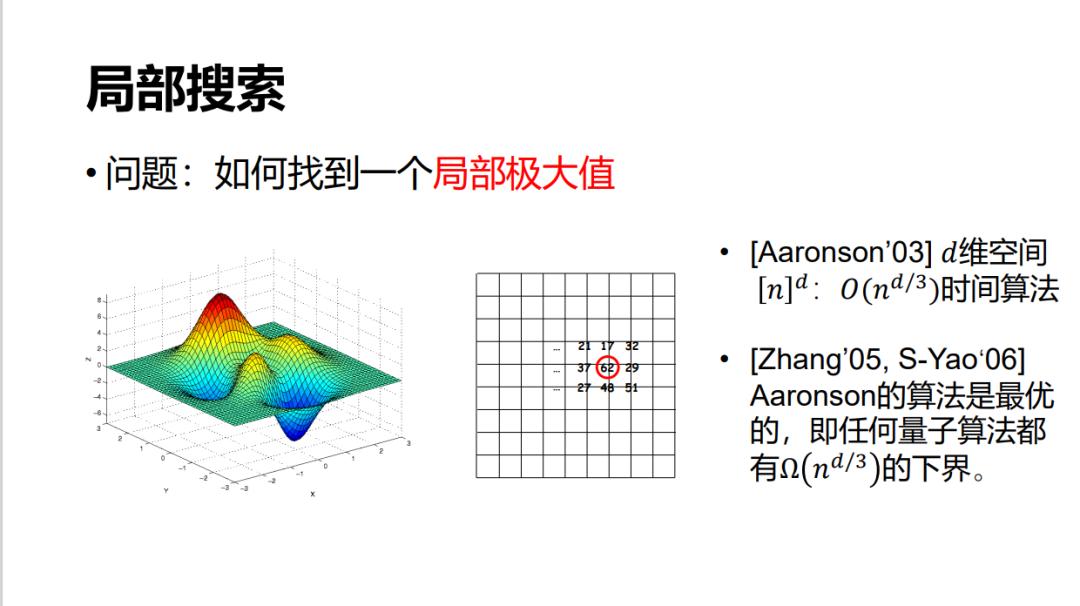
下面介绍我与胜誉以前共同做的一个工作:Grover 搜索可以用来解求全局极值,即需要根号 n 的时间就可以找到一个全局极大值或极小值。如果我们只需要找一个局部极值,譬如在机器学习里有很多应用,很多时候其实找一个局部极值就可以。
Aaronson 最早研究了这一问题并给出了一个基本上可以做到开三次方的算法。胜誉、姚老师和我一起证明了,这个开三次方的加速就是最好的了。
权重判定
下面分享一下我们最近做的一个小工作,称为权重判定问题。它需要区分这样两种情况,即解的个数或者有 k 个或者有 l 个,k 和 l 是事先给定的两个数。其他的情形都不管,只需要能区分这两种权重就行。
我们可以看到一些特例,譬如说 k 等于 0,l 等于 n/2,即恰好有一半解还是一个解都没有。这个就是最早提出的第一个量子算法,即 Deustch-Josza 算法要做的事情。再譬如 k 等于 0,l 等于 1,区分有没有至少一个解,这个就是 Grover 算法做的事情。

其实在我们之前,中山大学的邱道文老师他们做过一些工作,另外其他研究者也做过一些工作,这里不再一一赘述。

主要结果
接下来直接说一下我们的结论,我们给出了一个下界和一个上界。这里我用图来说明上下界分别是什么样子。
右上图说的是上界,也就是一个量子算法。对于不同的参数 d,我们可以首先生成一批点,譬如之前的工作能做的区域只有绿色、红色以及这些点(中间图)。我们基本上把所有的区域都解决了,比如说 d=2 的时候有两个点(右上图),这两个点它左上都只需要 1 次量子查询,就和(左图)绿色的一样。
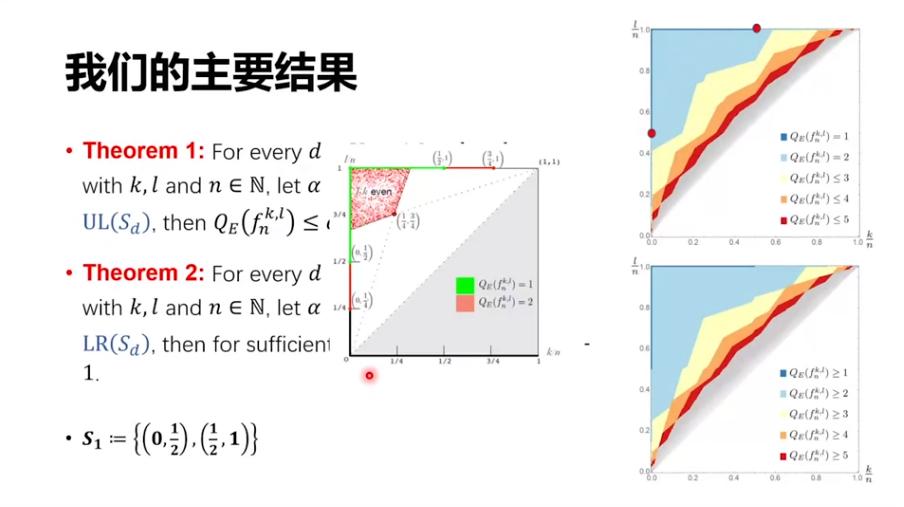
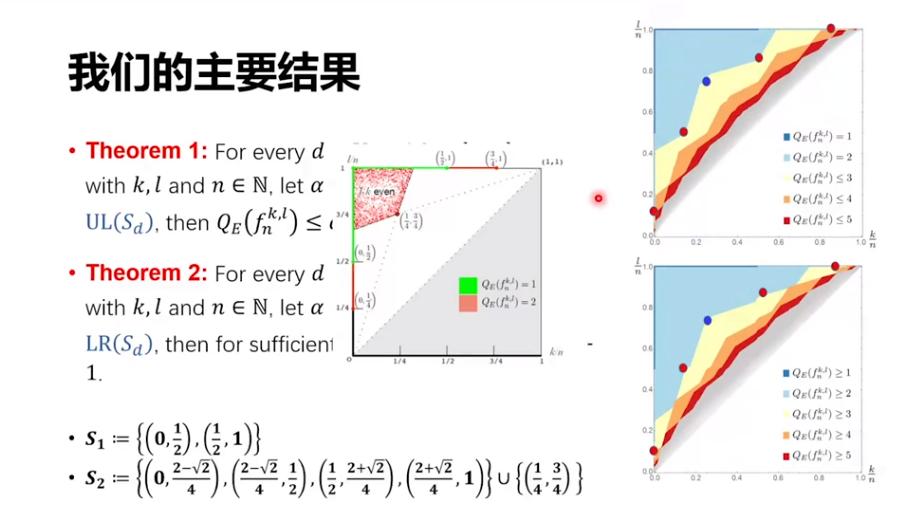
再下一个 Case 有 5 个点,就是下面右上图中的 4 个红点和 1 个蓝点。它的左上方的浅蓝色区域,量子只需要两步就可以解决,完全覆盖了之前的一些结论。同时,这 5 个点的右下方,也就是右下图浅黄色这片区域。我们可以证明,它们是不可能用量子两步解决的,至少要三步。
然后,我们进一步定义集合 S_3,即有另一批点。它的左上方有一个算法可以 3 步做成,它的右下方任何算法至少要 4 步才能做成,类似可以推广到任意的d。
刚才胜誉的工作也提到了我以前的博士生袁佩,这个工作是和袁佩博士、现在的一个博士生何啸宇以及前同事杨光一起做的。
量子复杂性下界
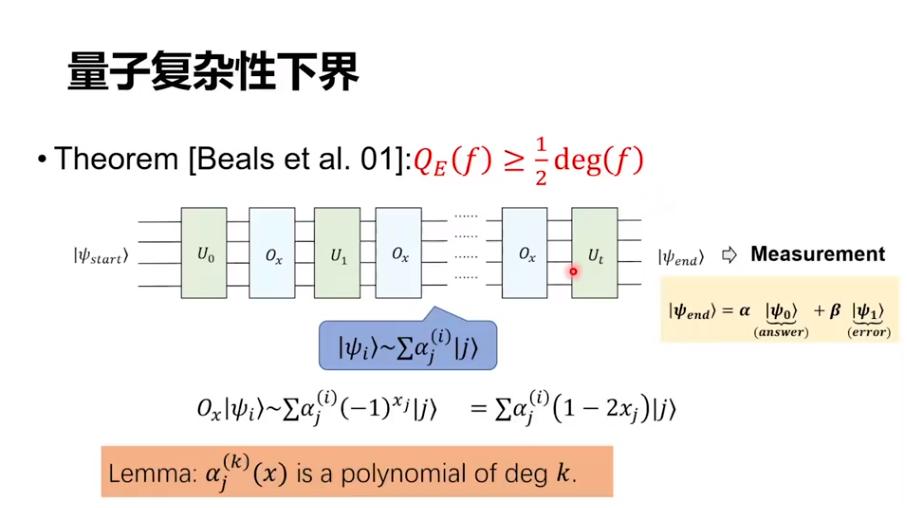
同时我们还做了一个下界,也就是说,我们可以证明在一些区域上量子不能做得特别好。其中最核心的一个定理是 2001 年 Beals 等人证明的一个结论,对精确量子算法,它的复杂度可以被这个函数写成一个多项式后它的 Degree 除以 2 给出一个下界。所以,我们就可以把这个问题转化成去考虑它的多项式表示的多项式次数。
研究多项式次数需要用到一些工具,这里有一个很著名的多项式叫切比雪夫多项式(Chebyshev Polynomials),就是说 cos mθ(m 是一个整数)都可以写成 cos θ的一个多项式,比如根据二倍角公式
,cos 3θ可以写成
,等等。

Grover 搜索背后的关键其实也是这样一个切比雪夫多项式。我们在这个工作中也要用到它,最关键的一点就是切比雪夫多项式构成了多项式空间的一组基。接着我们把任何一个多项式展开到这组基上,再利用切比雪夫多项式的一些性质证出来一个下界。

带先验知识的量子搜索
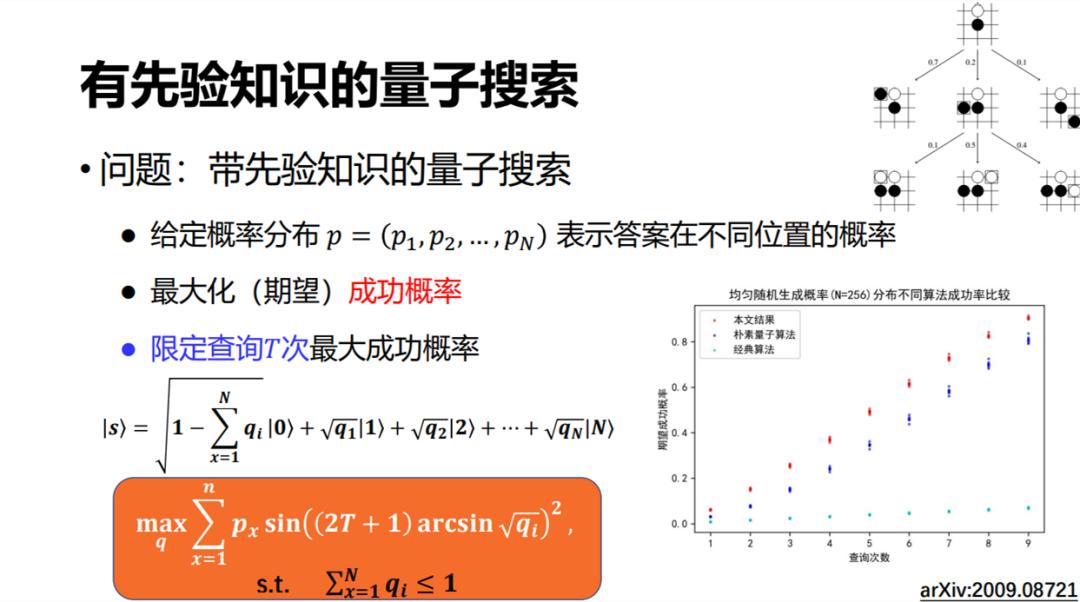
下面介绍我们最近做的另一个工作,称为带先验知识的量子搜索。由于在 Grover 搜索中,我们对想要找的解一无所知,也就是说它是任何一个的概率都是相等的。但在有些搜索问题里,比如α-β剪枝,我们事先知道一定的概率分布,即走哪条路的概率更高一点。
假如我们现在把它建模成 p = (p_1, p_2, …, p_N) 的形式,我们知道 1 是解的概率是 p_1,2 是解的概率是 p_2,N 是解的概率是 p_N。在这种情况下怎样做一个最好的搜索呢?我们最近研究了这个问题,大概的核心结论是需要制备一个特殊的初态,这也是后来我们跟胜誉一起讨论初态制备问题的出发点之一。
制备了这个特殊的初态之后,后面的算法步骤(对称、翻转等)跟 Grover 算法很像。我们可以证明,这样做在渐进意义上几乎是最优的。
电路优化
下面再简单介绍一下量子电路优化方面的工作。最近,量子硬件发展很快,John Preskill 教授在 2018 年提出了一个概念,叫做 NISQ(含噪声、中等尺度量子系统)。刚才胜誉也提到 IBM 有个路线图,称明年就可以做到 1000 多个比特。但是,它的特点是噪声很大,所以需要压缩电路的深度。

之前我们做了这样一个工作,就是去讨论 CNOT 电路的线路深度。众所周知,CNOT 加上单比特门就是 Universal 的,可以生成任何的量子电路。所以,CNOT 电路有一定的重要性。
下面是一个例子,说明一个 CNOT 电路可以转成一个等价的电路。原来的深度是 7,现在深度是 5。最核心的一点是,CNOT 电路本质上可以写成这些变量的一个线性组合。
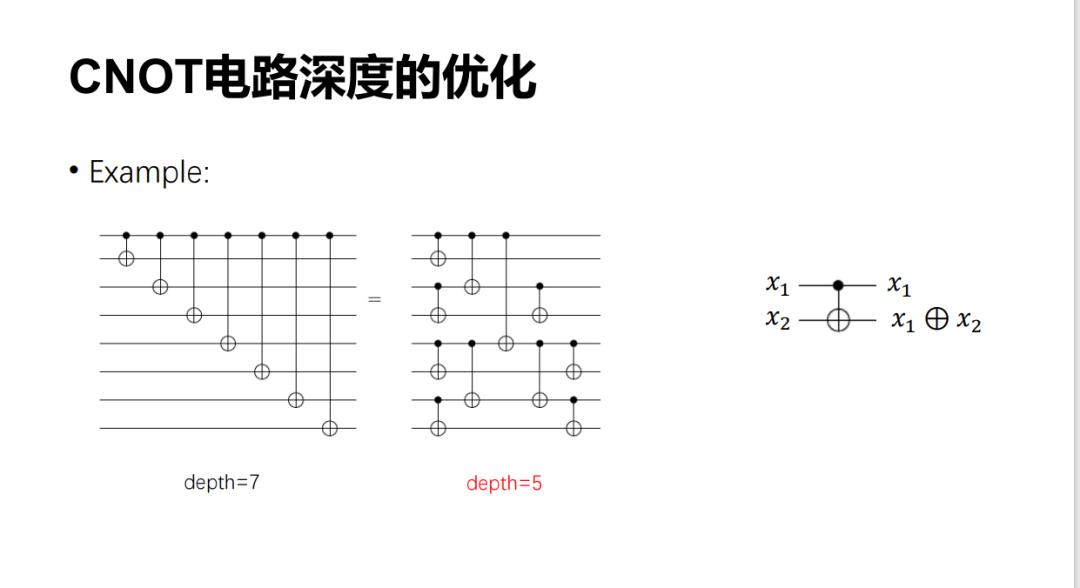
CNOT 电路的化简其实和 F_2 上的可逆矩阵分解有重要联系。事实上,我们在每一层上可以放多个 CNOT 门,譬如下面左下图第一层放了两个 CNOT 门,它对应右下图第二个矩阵。从线性代数上,可以将它看作一个行消元,即把第一行加到第二行,第三行加到第四行。

所以,CNOT 电路的化简可以变成这样一个数学问题,即如果允许并行的高斯消元,要把一个可逆的矩阵化成单位阵,最少需要多少步?注意每一步可以并行地来做。

结果介绍
我们做了如下一些结果,主线是讨论辅助比特和电路深度之间的关系。
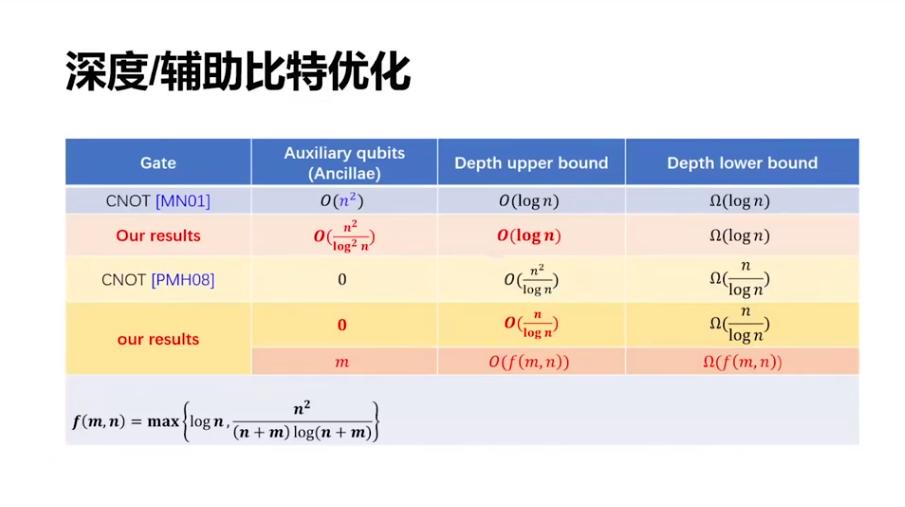
这是之前的结果,辅助比特达到 n^2 的时候有一个结果,辅助比特为 0 的时候也有一些结果。我们可以把两边的结果都加以改进,而且还有一个更一般性的结果,就是如果有 m 个辅助比特,那么这个电路深度可以优化到一个紧的界,即下图右下方的表达式。特别的当 m 等于 0 和 m 等于 n^2 的时候,我们的结果分别可以把原来的两个界优化一些。
团队及书籍介绍
下图中是我们中科院计算所量子计算与算法理论实验室团队的一部分成员,包括刚才工作中提到的张家琳老师、田国敬老师、袁佩博士、蒋佳卿、何啸宇和杨帅等。
这次活动我们得到了两家出版社的大力支持。与尚云教授、李绿周教授、尹璋琦教授、魏朝晖博士、田国敬博士一起,我们花了三年时间翻译了量子计算领域最经典的一本教材,即 Michael A. Nielsen 和 Isaac L. Chuang 合著的《量子计算与量子信息》(10 周年版)(Quantum Computation and Quantum Information 10th Anniversary Edition) ,译著共 570 多页。
我们觉得它是一本非常优秀的教材,即使从现在的角度来看。当然,这本书确实缺少一些比较近期的(比如在硬件实现方面)内容。但是它作为入门教材对读者非常友好,特别是如果你从属于计算机领域,并且想要学习量子计算,那么你只需要掌握最基本的线性代数知识,阅读这本书就完全没有问题。